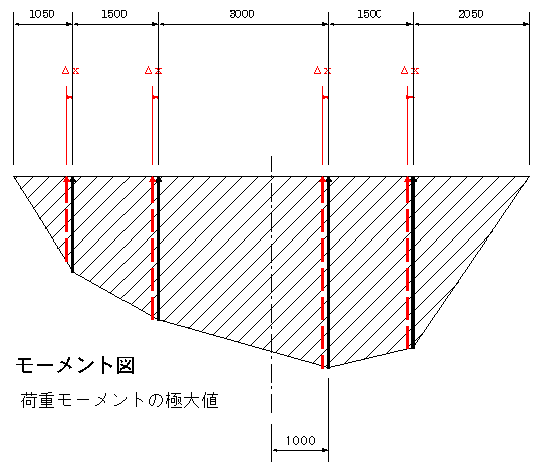
最大モーメントの荷重分布の求め方（モーメントの微分法）

後輪部がセンターから1.0ｍシフトしたケースを初期設定とする。
このときのＡ点の反力をＲa0、後輪部のモーメントをＭ0とする。

• Ｒa0＝1/9.1×｛Ｐr（8.050+3.550）＋Ｐf（6.550+3.550）｝
• Ｍ0＝Ｒa0×5.55−Ｐr×4.50−Ｐf×3.00
  

さて、３台の２ｔトラックがΔx移動した場合は反力はＲa(Δx)で後輪部のモーメントはＭ0(Δx)となる。

• Ｒa(Δx)＝1/9.1×｛Ｐr（8.050+Δx+3.550+Δx）＋Ｐf（6.550+Δx+3.550+Δx）｝
  ＝Ｒa0＋2/9.1×（Ｐr＋Ｐf）×Δx
• Ｍ(Δx)＝Ｒa(Δx)×（5.55−Δx）−Ｐr×4.50−Ｐf×3.00
  ＝｛Ｒa0＋2/9.1×（Ｐr＋Ｐf）×Δx｝×（5.55−Δx）−Ｐr×4.50−Ｐf×3.00
  ＝5.55Ｒa0−4.50Ｐr−3.00Ｐf＋｛Ｒa0−2×5.55/9.1（Ｐr＋Ｐf）｝Δx−2/9.1（Ｐr＋Ｐf）Δx＾2

Ｍ0(Δx)の最大値は、この関数の極大値を求めることとなるので、微分（勾配）が0になるΔxを求める。

• d/dx（Ｍ(Δx)）
  ＝d/dx［5.55Ｒa0−4.50Ｐr−3.00Ｐf＋｛Ｒa0−2×5.55/9.1（Ｐr＋Ｐf）｝Δx−2/9.1（Ｐr＋Ｐf）Δx＾2］
  ＝Ｒa0−2×5.55/9.1×（Ｐr＋Ｐf）−4/9.1×（Ｐr＋Ｐf）Δx
  ＝0（極大値の微分値は0となることより）

この式より

• Δx＝9.1/4/（Ｐr＋Ｐf）×｛Ｒa0−2×5.55/9.1×（Ｐr＋Ｐf）｝

Ｐr＝1.07、Ｐf＝0.27、Ｒa0＝1.664を代入して

• Δx＝0.009≒0.01ｍ